Wartość bezwzględna część II

W poprzednim poście zrobiłam wprowadzenie do tematu wartości bezwzględnej. To teraz czas na nierówności. Mamy np. taką nierówność:

Ix+2I>3

Najpierw sprawdzamy co jest pod wartością bezwzględną. W tym przypadku mamy x+2. To wyrażenie spod wartości bezwzględnej przyrównujemy do zera i wyliczamy proste równanie. Czyli

x+2=0

x=-2

Teraz rysujemy oś liczbową i nanosimy na nią nasz wynik. W tym wypadku -2.

Ok. Mamy już oś, mamy już -2 na osi, teraz patrzymy co jest po drugiej stronie nierówności. W naszym przypadku jest liczba trzy. To te 3 musimy dodać do naszych -2 i odjąć od -2. Dlatego zaznaczyłam na powyższej osi po trzy kreski z każdej strony. Wyjdą nam liczby +1 i -5. Zaznaczmy to sobie na naszej osi, która teraz wygląda tak:

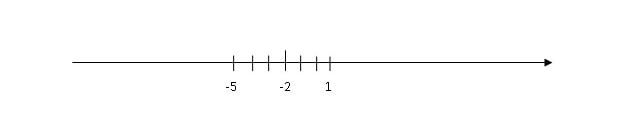
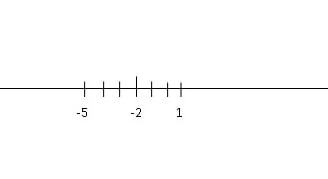
No dobra, to teraz ostatni etap rozwiązywania zadania. Wiemy już że po drugiej stronie nierówności mamy 3. Ale jaki jest znak nierówności? W naszym przypadku to > czyli znak większe. Pierwszą czynnością którą musimy zrobić to zaznaczyć na naszych liczbach -5 i 1 puste bądź pełne kółka. Puste kółko piszemy gdy znak jest < lub > oznacza to że -5 i 1 nie wchodzą do rozwiązania nierówności, a pełne kółka piszemy gdy znaki są ⩽ (mniejsze bądź równe) lub ⩾ (większe lub równe) i oznacza to że wchodzą do rozwiązania.

W naszym przypadku kółka będą puste. To jeszcze raz popatrzmy na naszą nierówność. Mamy Ix+2I > 3. Po prawej stronie nierówności jest > 3 Oznacza to że musimy znaleźć które liczby są w odległości większej od 3 od liczby -2. Takimi liczbami są np. liczba -10 , -7, 2, 8, 100 itp. Oznacza to się nstp. sposób:

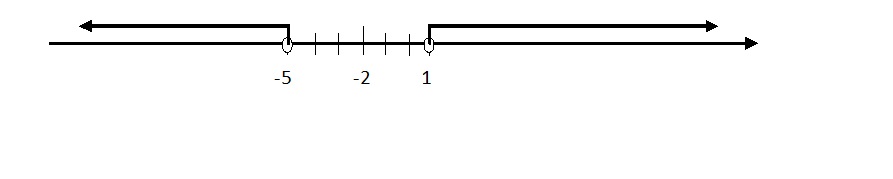
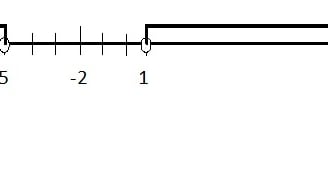
Teraz wystarczy tylko odczytać rozwiązanie. Pamiętaj!!! Rozwiązanie zawsze czytamy od najmniejszej liczby. W naszym przypadku rozwiązanie to:

x∈ (−∞; −5)υ(1; +∞)

Zwróć uwagę na nawiasy w rozwiązaniu . Wszystkie są otwarte. Przy czym przy symbolu +/-∞ nawiasy zawsze są okrągłe, a przy -5 i 1 dlatego że kółka są puste. A dlaczego są puste o tym pisałam powyżej.

Pierwszy przykład mamy za sobą. To jedziemy do następnego przykładu. Ix-4I≤1 Początek jest taki sam jak wyżej. Obliczamy równanie x-4=0 czyli x=4. Nanosimy tę czwórkę na oś. Teraz patrzymy co jest po prawej stronie nierówności. Jest 1, więc do 4 dodajemy 1 i odejmujemy 1. Wyjdzie nam odpowiednio 5 i 3. Teraz zaznaczamy te liczby na osi. Musimy teraz zaznaczyć kółka na osi. W tym wypadku kółko będzie pełne bo mieliśmy znak nierówności ≤ (mniejsze bądź równe).

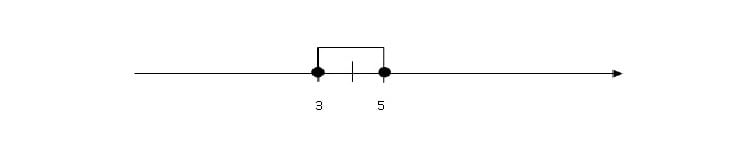
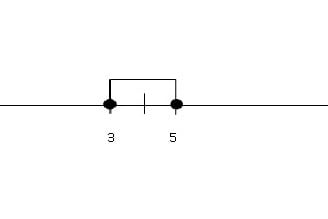
I na koniec musimy się zastanowić jakie liczby są w odległości mniejszej bądź równej niż jeden od liczby 4. Są to liczby min. 4,5, 4,75, 3,25 czy 3. Zatem nasza oś będzie wyglądać tak:

Czyli nasze rozwiązanie to wszystkie liczby od 3 do 5. 3 i 5 też są rozwiązaniem ponieważ był znak ≤, dlatego też rozwiązanie (wpisałam je poniżej) piszemy w nawiasach domkniętych. x∈< 3; 5 > Zwróćcie uwagę, że jeżeli znak nierówności jest > lub ≥ to strzałki rozchodzą się na zewnątrz i rozwiązanie jest sumą przedziałów od -∞ do jakiejś liczby suma jakaś liczba do +∞ np. tak jak w powyższym przykładzie x∈ (−∞; −5)υ(1; +∞)

Jeżeli jednak znak nierówności to < lub ≤ to wtedy strzałki schodzą się ze sobą i mamy jeden przedział np. x∈< 3; 5 >

Teraz powinno paść pytanie, a co się stanie jeśli po prawej stornie nierówności jest liczba ujemna? Już tłumaczę.

Musimy rozpatrzyć dwa przypadki:

Ix-5I>-1 

Ix-5I<-1

W pierwszym przypadku musimy sobie zadać pytanie: Jakie liczby na których nałożymy wartość bezwzględną będą większe od -1? Odpowiedź to wszystkie czyli x∈ 𝑅, ponieważ opuszczając wartość bezwzględną pozbywamy się minusa i mamy liczbę dodatnią, która jest zawsze większa od liczby ujemnej.

W drugim przypadku pytanie jest troszkę inne: Jakie liczby na których nałożymy wartość bezwzględną są mniejsze od -1 jeden. Odpowiedź to żadne czyli x∈

Zapamiętaj!

Jeśli mamy znak > (większe) a po prawej stronie nierówności jest liczba ujemna to rozwiązaniem x∈ 𝑅.

Jeśli jest znak <(mniejsze) a po prawej stronie nierówności jest liczba ujemna to rozwiązaniem jest x∈